Ainolabs talks about systems, entities that are operated for defined purposes and with expectations of generating value to their developers, owners, users and other stakeholders. Value depends on the business case. The cost can be estimated, and we’ll get to this formulaic expression below:
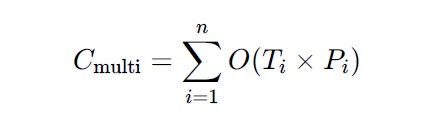
Systems are developed, launched, updated, supported and eventually replaced or discarded. They have a life span, and with life span there is the life time cost. We try to estimate that on a somewhat abstract level of complexity, as discussed in Computer Science.
There are two ways to build an AI system. One is the current, train everything in a single model, possibly create agent instances in that, package the model and release and run.
It is also possible to build a system of interconnected smaller models, minimodels. That is cost effective when the system functionality splits into disjoint subdomains, and especially if the combined dataset would have very low entropy, or, put in signal processing terms, signal to noise ratio (SR) is very low in the aggregate data set, but high in the parts when compartmentalized.
Building a system with many models incurs general overhead. In the Ainolabs architecture that means the burden of Content Classifier. This adds to the processing of each input, and should be balanced by the reduced cost of processing in the separate models (Learning Processes).
Scientish-like complexity estimates of development
By AI system we mean a system that uses Machine Learning technology as an essential element. A system could be built, as mentioned above as a monolith, or as a collection of separate smaller models. The development of an ML (AI) system is mostly related to training, and so the following estimates the order of magnitude costs of that.
We’ll use the following terms:
- T = number of training examples
- d = feature dimension per example
- P = number of model parameters (often ≈ scale of the model)
- E = training epochs / outer iterations (or rounds/trees, etc.)
- k = clusters or neighbors (when relevant)
- F = per-example forward+backward FLOPs (architecture-dependent; ≈ proportional
to P for dense nets)
In machine learning, P represents the total number of trainable parameters — the variables
that the training process adjusts to minimize loss.
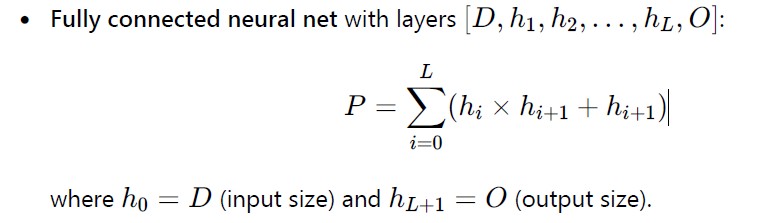
Taking noise into account
The number of parameters in the model, P, depends on the quality of the data. This has an impact on the model, training and semantic model capacity. Data with a lot of noise and no signal results in a very easy model, but with no practical value – just consider the ultimate white noise, cosmic background 4K radiation. P is conceptually a measure of information in a model.
If the training data as an aggregate is noisy – e.g. different sensory systems for different purposes look like noise when combined – splitting it might help.
Next we try to create a way to express and predict P in terms of dataset characteristics like size T , signal-to-noise ratio (SR), and desired accuracy A.
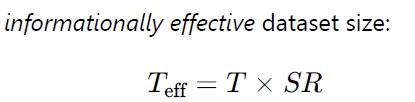
For that we need to define
For a model the number of parameters P needed is roughly proportional to the amount of true signal in your data and inversely proportional to the noise and desired accuracy.

We’ll skip a few steps and claim that the number of parameters is proportional (“Oh”-notation) to the size of the corpus T, signal to noise ration SR, and desired accuracy A. Exponents depend on the specific situation:
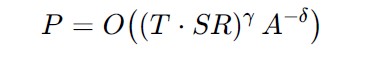
And with that it is possible to express the order of magnitude of training a model as
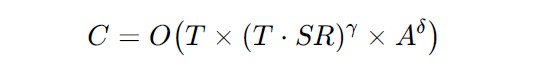
Divide et impera, or split the system into parts
The full dataset T might be large, could consist of orthogonally different data (audio, video, and temperature, for example). In such a case it would make sense to split the task – LP1, LP2 etc in the architecture.
Next total dataset has size T, and it is divided it into disjoint subsets:
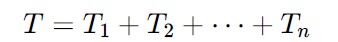
Training cost for comparison between a monolith and multimodel system are
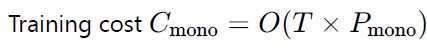

With these two it is possible compare the effectiveness of different or combined data sets for an operational system that utilizes Machine Learning technology – an AI system.